| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- pdf parsing
- 활성화함수
- 오차역전파
- 활성화 함수
- rag parsing
- LLaVA
- Cross Entropy Error
- 파인튜닝
- 합성곱 신경망
- fine tuning
- 데이터 파싱
- fp32
- 딥러닝
- LLM
- bf16
- Nested Learning
- deep learning
- 이상탐지
- qlora
- gemma3
- multi-query
- Non-Maximum Suppression
- anomaly detection
- rrf
- fp16
- Time Series
- visual instruction tuning
- rag-fusion
- LLM 패러다임
- Mean squared error
- Today
- Total
Attention, Please!!!
딥러닝의 학습 #2.1 (Optimizer 종류와 학습) 본문
※ 앞선 포스팅에서 딥러닝의 학습(Backpropagation) 에 대해 소개하였습니다. 숨긴 글 참조 부탁드리겠습니다!
본 게시물에서는 신경망의 효율과 정확도를 높이는 방법인 옵티마이저(Optimizer)의 종류에 대해 알아보도록 하겠습니다.
SGD의 단점
신경망 학습의 최종 목적은 손실 함수의 값을 최대한 낮게 매개변수를 찾는 것 입니다. 즉 매개변수의 최적값을 찾는 것이며, 이를 최적화(Optimization)이라고 합니다. 앞선 포스팅에서는 매개변수 값을 찾기 위해 기울기(미분)를 사용하여, 값을 점진적으로 갱신하는 확률적 경사하강법 등 외를 사용했습니다. SGD는 단순하고 구현하기 매우 쉽지만, 문제에 따라서 비효율적일 때가 있습니다.
1. 비등방성 함수
아래의 사진을 통해 예를 들어보겠습니다.

이와 같은 사진에서 보이는 기울기는 y축 방향은 크고 x축 방향은 현저히 작습니다. 또한, 최솟값이 되는 장소 (x,y) = (0,0) 이지만, 기울기 대부분은 (0,0) 방향을 가르키지 않습니다.
그렇다면, SGD의 초깃값을 (x,y) = (-7.0, 2.0)으로 설장하고 적용한다면 무슨 일이 발생할까요?

SGD에 의한 최적화 갱신경로는 위와 같이 지그재그로 이동하면서 최솟값인 (0,0)에 비효율적으로 도달하는 것을 볼 수 있습니다. SGD의 단점은 비등방성* (Anisotropy) 함수 에서 탐색 경로가 매우 비효율적입니다.
*비등방성 함수 : 특정한 좌표에서 기울기의 성질 (기울기가 가르키는 지점)이 변하는 경우
2. Saddle Point

위의 그림에서 검은색 점을 Saddle Point (안장점) 이라고 합니다. 안장점은 기울기가 0이지만 극값이 아닌 지점을 뜻 합니다. 즉, 어느 방향에서 보면 극댓값 (C-D) 이고 다른 방향에서 보면 극솟값 (A-B) 이 되는 점 입니다. 따라서 해당 지점은 미분이 0이지만 극값을 가질 수 없습니다. 경사하강법은 미분이 0일 경우 더이상 파라미터를 업데이트 하지 않기 때문에, 이러한 안정점을 벗어나지 못하는 한계가 있습니다.
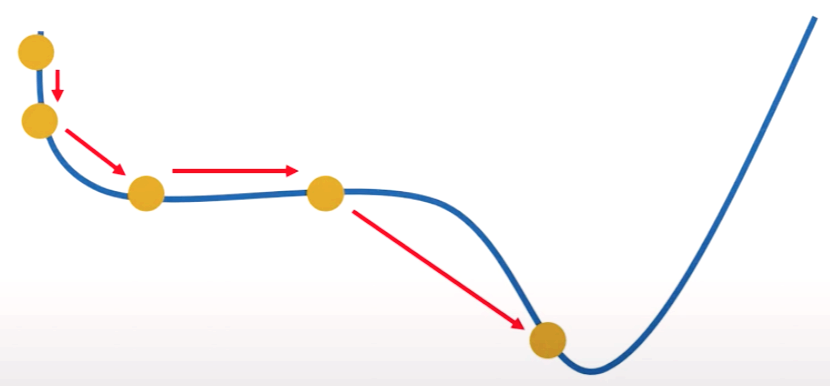
3. Local Minimum

위 그림의 Non-Convex 함수는 위치에 따라 파라미터의 최적 값이 달라지므로, Local Minimum에 빠져 최적의 값을 도출하지 못하는 경우가 많습니다. 또한, 평평한 곳으로 파고드면서 학습이 진행되지 않는 정체기에 빠질 수 있는 위험이 있습니다.
이러한 SGD의 파라미터 변경 폭이 불안정한 문제를 해결하기 위해 학습 속도와 운동량을 조절하는 옵티마이저(Optimizer)를 적용해볼 수 있습니다.
옵티마이저(Optimizer)의 종류
▶ 모델의 파라미터를 조정하면서 손실 함수가 최소화되도록 하는 것.

1. 모멘텀 (Momentum)
경사하강법과 같이 매번 기울기를 계산하지만, 가중치를 수정하기 전에 이전 수정방향을 참고하여 같은 방향으로 일정한 비율로 수정하게 됩니다. 이전 이동 값을 고려하여 일정 비율만큼 다음 값을 결정하는 관성 효과로 인하여 Saddle Point (안장점)이라는 문제점을 극복할 수 있습니다.
확률적 경사 하강법 수식이 다음과 같다고 하겠습니다.
이때
수식을 통해서 가중치를 업데이트 하게 되는데, 기울기 크기와 반대 방향만큼 가중치를 계산하게 됩니다. 쉽게 말하자면 기울기가 (+)라면, (-) 방향으로 업데이트하는 셈이죠. 또한, 모멘텀은 확률적 경사하강법에서 기울기
를 속도 (v)로 대처하여 이전 속도의 일정부분을 반영하게 됩니다. 이에 모멘텀의 수식은 아래와 같아 집니다.
즉, 모멘텀 옵티마이저는 이전에 학습했던 속도(기울기)와 현재 기울기를 반영해서 이동하기에 Local Minimum에 빠질 경우가 거의 없습니다. 하지만 멈추어야 할 시점에서도 관성으로 의해 훨씬 멀리 갈 수 있다는 단점이 있습니다. 이를 고안하기 위해 네스테로프 모멘텀이 개발되었습니다.
2. 아다그라드 (Adagrad, Adaptive Gradient)

경사하강법은 오차를 가장 적게 만드는 방향으로 가중치를 업데이트 하면서 최적의 값을 찾는 방법입니다. 하지만 이렇게 파라미터의 최적 값을 찾는 문제는 신경망의 최종목표이기도 하지만 매우 어려운 문제입니다. 이를 해결하기 위해서는 학습률 (learning rate)를 적절하게 지정해야 합니다. 이에 학습률을 작게 설정한다면, 학습시간이 오래 소요됩니다. 그렇다고 학습시간을 줄이기 위해 학습률을 크게 설정한다면, 수렴지점에서 좀 더 정확한 minimum 값을 찾지 못하고 Local Minimum에 빠질 위험이 상당히 큽니다. 이러한 학습률을 효과적으로 정하는 기술로 학습률 감소 (learning rate decay) 라는 것이 있습니다.

Adaptive Gradient는 변수(가중치)의 업데이트는 다음과 같이 이루어집니다. 많이 변화하지 않는 (기울기가 적은) 변수들의 학습률을 크게 설정하고, 많이 변화하는 (기울기가 높은) 변수들의 학습률을 작게 설정하는 것 입니다. 즉, 큰 보폭으로 산을 성큼성큼 걸어가다가 극솟값에 다가갈 때쯤부터 보폭을 줄여 살금살금 접근하는 방식과 같습니다.
Adaptive Gradient의 수식을 알아보도록 하겠습니다.
변수의 가중치마다 다른 학습률을 설정하기 위해 G함수가 추가되었습니다. 변수 G는 상태가 변할 때마다 기울기의 제곱 값이 계속해서 더해지는 것으로 기울기 크기의 누적된 값 입니다. 기울기가 크면 G값 또한 커지게 때문에
에서 학습률은 작아지게 됩니다.
즉, 파라미터가 충분히 학습되었다면 작은 학습률로 업데이트를 하고, 덜 되었다면 높은 학습률로 업데이트 하게 되는 것 입니다. 하지만 기울기의 누적된 값이 지속적으로 증가하고 이를 학습률로 나눈다면, 기울기가 0에 수렴하는 문제가 발생하게 됩니다. 이를 고안하기 위해 RMSProp이 개발되었습니다.
3. 아담 (Adam, Adaptive Moment Estimation)
아담 옵티마이저 같은 경우, Momentum 및 Adagrad 상위버전 (RMSprop)결합한 경사하강법 입니다. RMSprop 특징인 기울기의 제곱을 지수 평균한 값과 모멘텀의 특징인 v(i)를 수식에 활용하여 가중치를 업데이트 하게 되는것이 아담입니다.
'Deep Learning 이해' 카테고리의 다른 글
| 딥러닝의 학습 #2.3 (배치 정규화) (1) | 2024.02.06 |
|---|---|
| 딥러닝의 학습 #2.2 (가중치 초깃값-Xavier&He) (0) | 2024.01.16 |
| 딥러닝의 학습 #1 (Backpropagation) (0) | 2023.12.05 |
| 딥러닝의 구조 #4 [경사하강법] (0) | 2023.11.23 |
| 딥러닝의 구조 #3 [손실 함수] (0) | 2023.11.20 |




