| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 오차역전파
- gemma3
- fp32
- pdf parsing
- 합성곱 신경망
- multi-query
- LLaVA
- visual instruction tuning
- rag parsing
- rag-fusion
- Mean squared error
- Time Series
- fine tuning
- 데이터 파싱
- 이상탐지
- 파인튜닝
- rrf
- bf16
- Cross Entropy Error
- LLM
- anomaly detection
- LLM 패러다임
- fp16
- Non-Maximum Suppression
- 활성화함수
- 활성화 함수
- deep learning
- Nested Learning
- qlora
- 딥러닝
- Today
- Total
Attention, Please!!!
[개념 정리] Diffusion Model 본문
💡 Diffusion Model 이란?
2015년도에 “Deep Unsupervised Learning using Nonequilibrium Thermodynamics”이라는 논문으로 Diffusion Model이 처음으로 등장하였습니다. 본 논문의 저자들은 Diffusion Model를 다음과 같이 설명하였습니다.
The essential idea, inspired by non-equilibrium statistical physics, is to systematically and slowly destroy structure in a data distribution through an iterative forward diffusion process. We then learn a reverse diffusion process that restores structure in data, yielding a highly flexible and traceble generative model of the data.
논문에서 발췌된 내용을 간략하게 번역해 보자면, forward diffusion process를 통해 데이터 분포의 구조를 변형시키고, reserve diffusion process를 통해 데이터의 구조를 복원하는 작업입니다. 이를 조금 더 직관적으로 생각해 보면, 두 개의 단계를 거쳐 "입력 이미지"와 "결과 이미지"의 확률 분포를 유사하게 만드는 것이라고 할 수 있습니다.
📌 Forward Diffusion Process

이미지 \(x_{t-1}\)에 분산 \(\beta _{t}\)를 갖는 소량의 Gaussian Noise를 추가하여 새로운 이미지 \(x_{t}\)를 생성하는 조건부 함수\(q\left(x_{t}|x_{t-1}\right)\)를 생성하게 됩니다. Diffusion Model은 특정 상태(t-1)가 현재(t)의 상태에 의존하는 Markov(마르코프) 특성을 가집니다. 이러한 성질을 수학적으로 표현하기 위해 조건부 확률이 사용되는데, 이를 아래와 같이 표현할 수 있습니다.

이러한 함수를 지속적으로 적용하면 위의 그림처럼 잡음이 점진적으로 커지는 이미지 시퀸스 \(x_{o},...\ ,\ x_{T}\)를 생성할 수 있게 됩니다. Noise 주입 정도 (\(\beta _{t}\)가 무한대로 갈 때, 최종 이미지 (\(x_{T}\))는 Isotropic Gaussian Distribution에서 샘플링된 것처럼 완전히 잡음이 있는 이미지가 생성이 됩니다. 그럼 최종적으로 Forward Process의 전체적인 과정을 아래의 수식처럼 정의할 수 있게 됩니다.
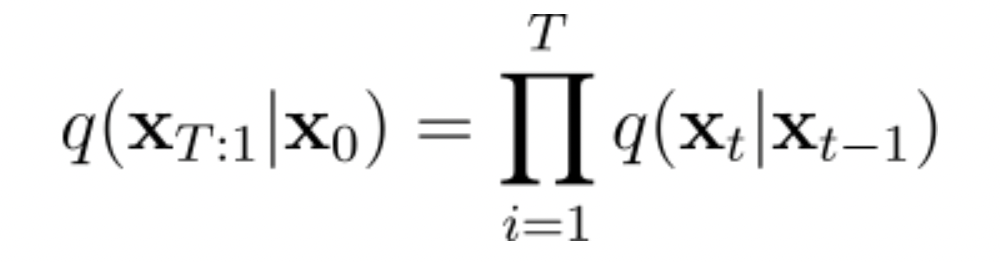
이때 (\x _{t}\)는 아래의 수식처럼 표현할 수 있습니다.
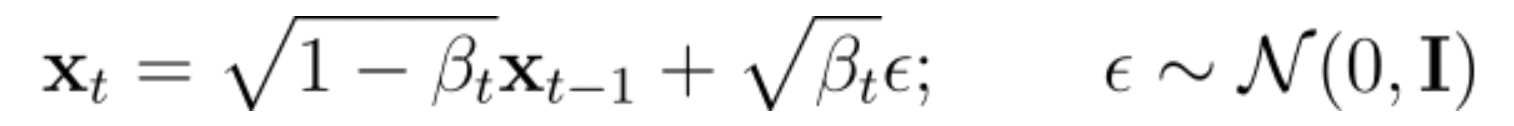
가 평균 \(\mu =0\)이고 분산 \(\sigma ^{2}=1\)인 정규분포에서 샘플링된 랜덤 변수라고 가정하겠습니다. 이제 새로운 변수 \(Y\ =\mu +\sigma x\)를 정의해 봅시다. Y의 기대값과 분산을 확인해보겠습니다.
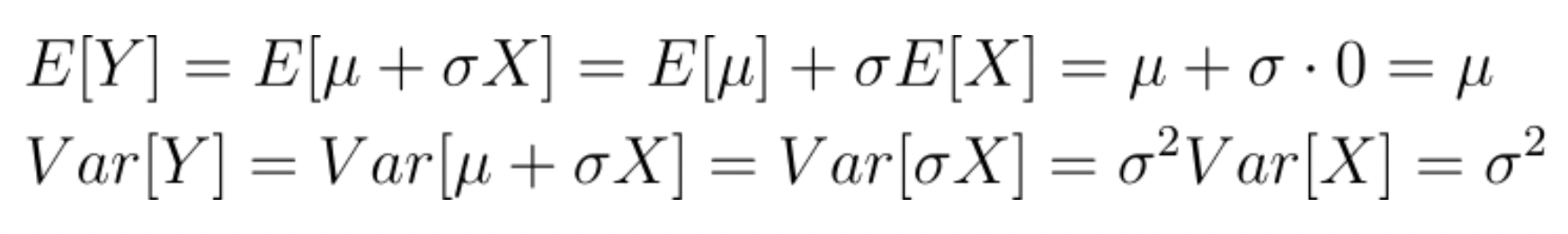
결과적으로 Y는 평군 \(\mu \)이고 분산 \(\sigma ^{2}\)를 갖는 가우시안 랜덤 변수입니다. 이에 똑같은 원리를 적용하게 되면, (\x _{t}\)는 평균 \(\sqrt{1-\beta _{t}}x_{t-1}\)이고 분산 \(\beta _{t}\)를 가지는 가우시안 랜덤 변수라고 정의할 수 있게 됩니다.
위의 과정을 통해 \(x_{t}\)는 평균이 0이고 분산이 1인 정규분포를 따르게 됩니다. 이는 모든 t에 대해 동일하게 적용되므로, T가 커질수록 \(x_{0}\)는 표준 가우스 분포에 점점 더 가까워지게 됩니다. 이는 이미지 시퀀스가 시간이 지남에 따라 점진적으로 정규화되어 표준 가우스 분포에 수렴하게 됩니다.
✔️ 재매개변수화 트릭(Reparameterization Trick)
Diffusion Model의 Forward Process의 목표는 입력 이미지 \(x_{0}\)에 점진적으로 노이즈를 추가하여 \(x_{T}\)에 도달하는 것 입니다. 이러한 과정은 아래와 같이 표현이 될 수 있다고 정의하였습니다.
\(q\left(x_{t}|x_{t-1}\right)=N\left(x_{t};\sqrt {1-\beta _{t} x_{t-1}},\beta _{t} I\right)\)
여기에서 생각해봐야 할 게 있습니다. 만약 q를 t번 iterative 하게 적용하지 않고 이미지 \(x_{0}\)에서 잡음이 있는 이미지 \(x_{t}\)로 바로 건너뛸 수 있는 알고리즘이 있다면, 굉장히 유용할 것입니다. 이때 사용하는 방법이 재매개변수화 트릭(Reparameterization Trick)입니다.
재매개변수화 트릭을 사용하면 아래와 같이 수식을 유도할 수 있습니다.
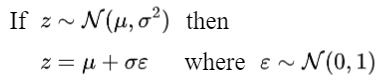
위의 언급된 것처럼, Diffusion Model은 마르코프의 특성을 기반으로 조건부 상태로 표현이 된다고 하였습니다. 이에 새로운 상태 \(x_{t}\)를 이전 상태 \(x_{t-1}\)와 잡음 \(epsilon_{t-1}\)을 기반으로 방정식을 아래와 같이 정의할 수 있으며, 여기에서 \(\beta _{t}\)는 시간에 따라 변화하는 가중치를 뜻합니다.
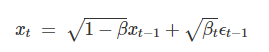
위의 두 성질을 아래와 같이 확장시킬 수 있습니다.

빨간색 상자의 수식은 정규 분포의 가법성에 따라 독립인 두 확률 변수 X와 Y를 더하면 \(Z\sim N\left(\mu _{x}+\mu _{y},\sigma _{x}^{2}+\sigma _{y}^{2}\right)\)으로 표현할 수 있습니다. 이것에 대해 구체적으로 궁금하시다면 아래의 숨긴 글을 참조해 주세요.

이러한 수학적인 과정을 거치게 되면, 입력 이미지 \(x_{0}\)을 알면 특정 상태의 노이즈를 파악할 수 있습니다.
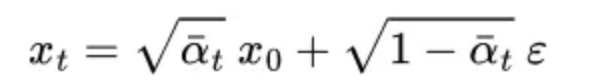
📌 Reverse Diffusion Process
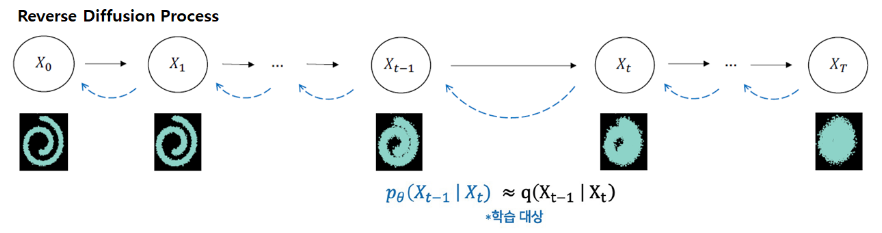
Reverse Diffusion Process는 gaussian noise를 제거하는 과정입니다. 그럼 정방향 과정에서의 조건부 확률 \(q\left(x_{t}|x_{t-1}\right)\)를 사용했던 거처럼 역방향 과정에서도 조건부 확률을 적용하면 될까요?
불가능합니다. 왜냐하면 확률 분포가 계산하기 어려운(intractable/uncomputable) 형태를 가지고 있기 때문입니다. 역방향 조건부 확률 \(q\left(x_{t-1}|x_{t}\right)\)를 계산하기 위해서는 전체 정방향 과정에서 축척된 모든 Noise의 영향을 반영해야 하는데 이러한 과정은 수학적으로 매우 복잡한 문제입니다.
\(q\left(x_{t}|x_{t-1}\right)\)의 역방향 분포를 근사화하는 신경망 \(p\theta \left(x_{t-1}|x_{t}\right)\)을 학습해야 합니다. 이때 \(p\theta \left(x_{t-1}|x_{t}\right)\)는 정규 분포를 따르며, 평균과 분산은 아래와 같이 정의할 수 있습니다.
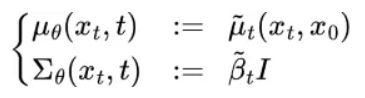
역방향 과정에서 모델 \(p_{\theta }\)을 학습하여 각 단계에서 Noise 생성 확률 분포 Parameter인 평균과 표준편차를 업데이트하며 학습이 진행하게 됩니다. 각 단계에서 노이즈를 제거하고 \(x_{t-1}\)를 추정하게 되는데, 이때 손실함수가 필요하게 됩니다. 다음 게시물에서 확인해주세요.
'Generative AI' 카테고리의 다른 글
| [개념정리] Diffusion Model Loss Function (0) | 2024.06.15 |
|---|
