| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Time Series
- bf16
- visual instruction tuning
- multi-query
- Cross Entropy Error
- Non-Maximum Suppression
- 합성곱 신경망
- qlora
- LLaVA
- 오차역전파
- rrf
- Nested Learning
- deep learning
- fp16
- 이상탐지
- LLM
- LLM 패러다임
- Mean squared error
- pdf parsing
- rag parsing
- 딥러닝
- fine tuning
- 활성화 함수
- rag-fusion
- 데이터 파싱
- gemma3
- 활성화함수
- 파인튜닝
- fp32
- anomaly detection
- Today
- Total
Attention, Please!!!
딥러닝의 구조 #1 [퍼셉트론] 본문
본 게시물은 공부목적으로 작성 되었으며, 밑바닥부터 시작하는 딥러닝 참고하였습니다.
퍼셉트론이란?
▶ 다수의 신호를 입력으로 받아 하나의 신호를 출력하는 것을 뜻합니다. 퍼셉트론의 신호는 흐름을 취합하고 만들면서 정보르 앞으로 보내게 됩니다. 하지만, 퍼셉트론 신호는 (0 or 1)의 두가지 값을 가질수 있습니다.
퍼셉트론의 구조를 배우는 것은 신경망과 딥러닝을 이해하는데 기반이 되기에 짚고 넘어가는게 중요합니다.

퍼셉트론이 동작하는 방식은 다음과 같습니다. Input들의 신호들이 뉴런으로 보내질 때는 각각의 고유한 Weight들과 곱합니다. 이렇게 계산된 신호의 총합이 활성함수 (Activation Function)에 의해 판단이 되는데, 그 값이 임계치 (한계) 보다 크다면 뉴런이 활성화되어 1이라는 Output을 출력하게 됩니다.
이를 수식으로 나타내면 다음과 같습니다.
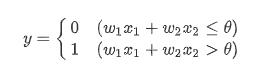
복수의 입력 신호 각각에 특정 가중치를 부여하게 됩니다. 가중치는 각 신호가 결과에 가장 큰 영향력을 주는 요소입니다. 이에, 가중치가 크면 클수록 해당 신호가 그만큼 중요한 것을 뜻합니다!
하지만, 1957년 프랑크 로젠블라트라는 사람에 의해 소개된 퍼셉트론에는 가장 큰 문제점이 있습니다.
위의 수식처럼, 초기의 퍼셉트론은 Unit Step을 통해 (0과 1이라는 결과 값만 도출하는) 필터링 기능밖에 없으므로, 학습 시에 배운다는 개념이 적용되기 어렵습니다. 이를 해결하기 위한 다양한 활성함수 (Sigmoid, ReLu 등) 소개됩니다. 이는 추후에 다뤄보도록 하겠습니다.
퍼셉트론의 한계 / 다층 퍼셉트론
저희는 여태까지 퍼셉트론의 개념에 대해 알아보았습니다. 하지만 시대가 점차 발전하면서, 기존 퍼셉트론에 대한 문제점들어나기 시작했습니다. 아래의 그림을 통해 살펴보겠습니다.
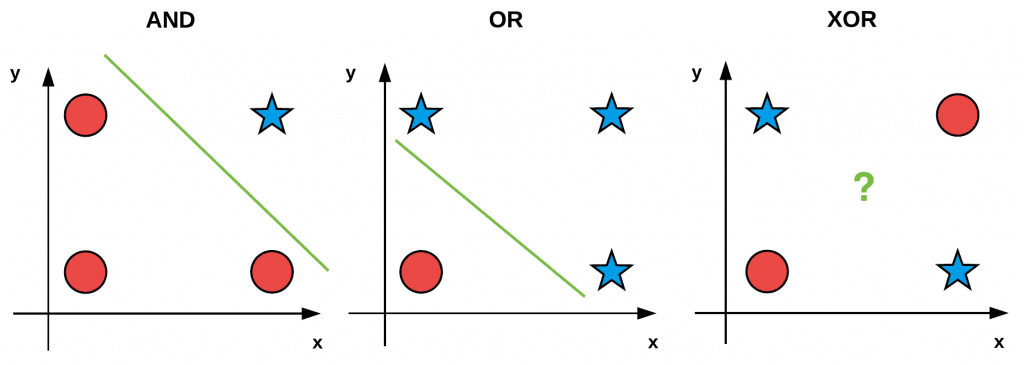

기존의 퍼셉트론으로 AND (+NAND) 및 OR 와 같은 연산을 통해 간단하게 구현할 수 있었습니다. 하지만 XOR연산은 두 개의 입력 값이 다르면 1, 같다면 0으로 출력이 됩니다. XOR 연산 같은 경우, 동그라미와 별을 단 하나의 직선으로 영역을 구분하는 것은 사실상 불가능합니다. 초기 퍼셉트론의 개념은 Unit Step 활성함수로 인하여, 0과 1이라는 결과 값만 도출할 수 있다는 단점이 존재했습니다.
즉, 단층 퍼셉트론은 직선 하나로 나눈 영역만 표현 가능할 수 있다는 한계가 있습니다.
그렇다면, 위의 사진과 같이, 곡선으로 비선형적인 영역에 대해 나눌수 있을까요?
이에 대한 한계점을 해결하기 위해, Marvin Minsky 교수는 Perceptrons 라는 책을 통해 XOR 문제를 기존의 퍼셉트론으로 해결할 수 없다는 것을 증명하였고, 다층 퍼셉트론이 XOR 문제점을 해결할 수 있다고 발표하였습니다.

XOR 연산이 기존 퍼셉트론의 개념으로 안되는 이유는 위의 그림과 같이 AND, NAND, OR 연산을 조합해야 가능하기 때문입니다. XOR 연산을 위해 입력층 및 출력층 사이에 은닉층을 별도로 구성하는 것 입니다. 입력층에서의 값을 기반으로 은닉층에서 NAND 및 OR 연산을 수행하고 결과값을 출력층으로 전달하게 됩니다. 출력층은 결과 값을 AND 연산하여 최종 값을 출력합니다. 이러한 개념은 다층 퍼셉트론 (Multi-Layer Perceptron)이라 칭합니다.
퍼셉트론의 원리 요약본
참고 부탁드리겠습니다!
퍼셉트론의 원리
활성화 함수에 Deep-Dive하기 앞서, 퍼셉트론의 원리에 대해 간략하게 알아보겠습니다.

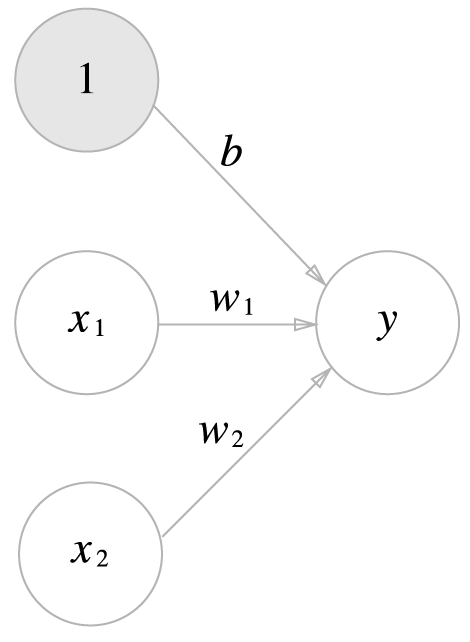
그림과 같이 퍼셉트론의 동작은 x1,x2, 1 이라는 3개의 신호가 뉴런에 입력되고, 각 신호에 가중치를 곱한 후, 다음 뉴런으로 전달되게 됩니다. 이러한 신호들의 합이 0을 넘으면 1을 출력하고, 그렇지 않는다면 0을 출력하게 됩니다.
이를 통해 단층 퍼셉트론 구조는 활성화 함수로 계단 함수를 사용한다는 것을 파악할 수 있습니다. 또한, 비선형적/선형적 영역을 구분하기 위해, Sigmoid 함수 등 여러가지의 활성화 함수가 소개 되었습니다.
'Deep Learning 이해' 카테고리의 다른 글
| 딥러닝의 학습 #2.1 (Optimizer 종류와 학습) (0) | 2023.12.18 |
|---|---|
| 딥러닝의 학습 #1 (Backpropagation) (0) | 2023.12.05 |
| 딥러닝의 구조 #4 [경사하강법] (0) | 2023.11.23 |
| 딥러닝의 구조 #3 [손실 함수] (0) | 2023.11.20 |
| 딥러닝의 구조 #2 [활성화 함수] (0) | 2023.11.09 |




