| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- LLM 패러다임
- 파인튜닝
- Nested Learning
- LLM
- 활성화 함수
- rrf
- fp32
- anomaly detection
- Non-Maximum Suppression
- 데이터 파싱
- rag-fusion
- 활성화함수
- qlora
- fp16
- rag parsing
- deep learning
- multi-query
- 합성곱 신경망
- 이상탐지
- 오차역전파
- pdf parsing
- bf16
- LLaVA
- Mean squared error
- gemma3
- 딥러닝
- fine tuning
- visual instruction tuning
- Cross Entropy Error
- Time Series
- Today
- Total
Attention, Please!!!
회귀분석이란? 본문
본 게시물은 공부목적으로 작성 되었으며, 파이썬 머신러닝 완벽 가이드 참고하였습니다.
회귀 분석이란?
▶ 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법
예를 들어, 아파트의 방 개수, 방 크기, 주변 학군 등 여러 개의 독립변수 (X 값) 에 따라 아파트 가격이라는 종속변수 (Y 값)가 어떤 관계를 나타내는지 모델링하고 예측 하는 것을 뜻합니다. 또한, 독립변수의 값에 영향을 미치는 회귀 계수 (W 값) 도 포함 되어있습니다.
이에, 머신러닝의 회귀분석 핵심은 주어진 피처와 결정 값 데이터 기반으로 최적의 회귀 계수를 파악 하는 것 입니다.
▶ 회귀분석의 유형
- 일반 선형 회귀: 예측값과 실제값의 RSS를 최소화할 수 있도록 회귀 계수 최적화
- Ridge 회귀 : 선형 회귀에 L2 Norm이 추가된 회귀 모델; 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해 회귀 계수값을 더 작게 만드는 규제 모델
- Lasso 회귀 : 선형 회귀에 L1 Norm이 추가된 회귀 모델; 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어, 피처가 선택되지 않게 하는 모델
- ElasticNet 회귀: Ridge & Lasso 회귀가 결합되어, 피처의 개수를 줄이고 계수 값의 크기를 동시에 진행 (피처가 많은 데이터에 용이)
- Logisitic 회귀 : 이진 분류에 사용되는 선형 모델
▶ 회귀분석의 평가지표
회귀분석으로 도출된 잔차를 평가할 때 주의할게 있습니다. 실제 값과 예측값의 차이를 단순히 더하거나 뺀다면 오류가 발생할 수 있습니다. 예를 들어, 실제 값이 "1" 이고 예측 값이 "-1" 이라면, 오류는 0이 됩니다. 이에 회귀 분석에서 오류를 평가할때는 절댓값 평균 및 제곱 등이 사용됩니다.
- Mean Absolute Error (MAE) : 실제 값과 예측 값의 차이를 절댓값으로 변환해 평균화한 것.
- Mean Squared Error (MSE) : 실제 값과 예측 값의 차이를 제곱하여 평균화한 것.
- Root Mean Squared Error (RMSE) : MSE 값은 오류의 제곱을 구하므로, 실제 오류 평균보다 더 커지는 특성이 있으므로 Root를 씌워 사용
- R-squared : 분산 기반으로 예측 성능을 평가함. 실제 값의 분산 대비 예측값의 분산 비율
▶ 단순 회귀분석

단순 회귀분석은 독립변수 1개, 종속변수 1개로 이루어진 가장 간단한 형태의 회귀분석 입니다.
위의 그림과 같이, 평수가 넓으면 주택 가격이 높아지는 경향이 있습니다. 주택 가격은 평수에 대해 선형의 관계로 표현할 수 있습니다. 이에 2차원 평면에서 특정 기울기와 절편을 가진 1차 함수식이 도출됩니다. 실제 주택 가격은 1차 함수 값에서 실제 값만큼의 오류 값을 뺀 (또는 더한) 값이 되는 것 입니다.
그렇다면, 최적의 회귀모델은 어떻게 만들까요???
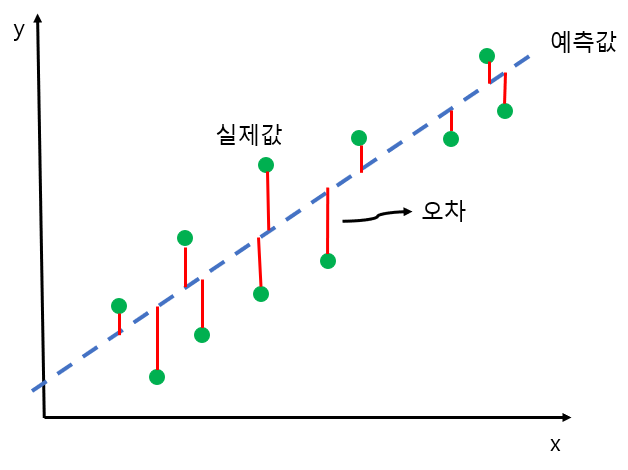
위의 그림과 같이 2차원 평면에는 초록색 점 (실제값) 과 파란색 실선 (예측값) 이 존재합니다. 이렇게 실제 값과 회귀모델으로 만들어진 예측 값에 대해 오차 (잔차)가 최소화 된다면, 최적의 회귀모델이 될 수 있습니다. 즉, 오류 값 합이 최소가 될 수 있는 최적의 회귀 계수를 찾는다는 의미로 바라볼수 있습니다.
▶ 다항 회귀분석
여태까지 다루었던 내용은 독립변수와 종속변수의 관계가 일차 방정식 형태로 표현될 수 있는 가장 간단현 형태의 회귀분석 이었습니다. 하지만 세상의 모든 관계는 일직선으로 표현할 수 없습니다. 단항식이 아닌 2차, 3차,..., n차 이루어진 다항 회귀분석이라고 합니다.
하지만...! 여기에서 주의할점이 있습니다. 다항 회귀분석에 대해 비선형 회귀로 혼동하기 쉽지만, 이는 선형 회귀에 해당됩니다. 회귀분석에서 선형/비선형 여부를 나누는 기준은 회귀 계수가 선형 or 비선형인지 따릅니다.
비선형인줄 알았는데, 새로운 Z라는 변수를 통해 아래와 같이 선형회귀로 표현할 수 있습니다.
예시)
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
import numpy as np
def polynomial_func(x):
y = 1 + 2*x[:,0] + 3*x[:,0]**2 + 4*x[:,1]**3
return y
#Pipeline 사용하면, 피쳐변환 및 선형회귀 적용 동시에 가능
model = Pipeline([('poly', PolynomialFeatures(degree = 3)),
('linear', LinearRegression())])
x = np.arange(4).reshape(2,2)
y = polynomial_func(x)
model = model.fit(x,y)
print('Polynomial 회귀 계수 \n', np.round(model.named_steps['linear'].coef_,3))

'Data Science > ML' 카테고리의 다른 글
| Bias-Variance Trade Off 이란? (0) | 2023.11.07 |
|---|

