| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- fp32
- 활성화함수
- 오차역전파
- Cross Entropy Error
- leetcode
- 파인튜닝
- qlora
- gemma3
- LLM
- rag parsing
- rrf
- visual instruction tuning
- deep learning
- 딥러닝
- Time Series
- 활성화 함수
- multi-query
- fine tuning
- Mean squared error
- Non-Maximum Suppression
- pdf parsing
- LLaVA
- bf16
- anomaly detection
- 데이터 파싱
- fp16
- 손실함수
- 합성곱 신경망
- 이상탐지
- rag-fusion
- Today
- Total
Attention, Please!!!
Bias-Variance Trade Off 이란? 본문
본 게시물은 공부목적으로 작성 되었으며, 파이썬 머신러닝 완벽 가이드 참고하였습니다.
편향-분산 Trade Off는 머신러니에서 꼭 집고 넘어 가야하는 중요한 이슈 중의 하나입니다.
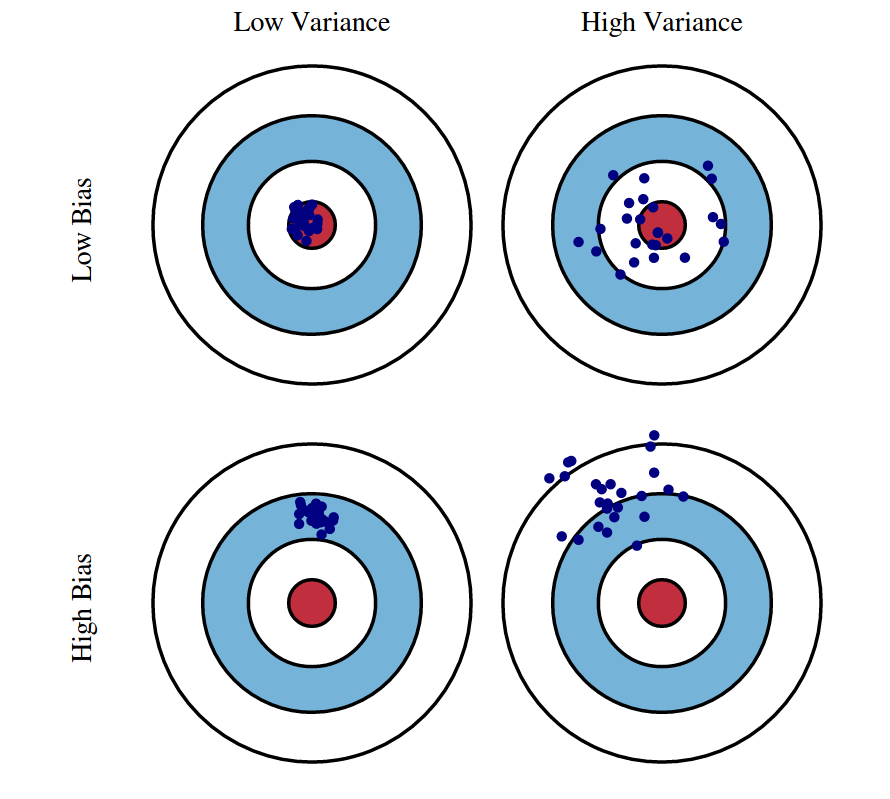
머신러닝에 대해 공부를 해보셨다면, 왼쪽의 양궁 과녁 그림은 익숙하실겁니다.
- 왼쪽 상단 : 예측 결과가 실제 결과에 매우 근접하고 예측 변동이 크지 않아, 아주 뛰어난 성능을 보임
- 오른쪽 상단 : 예측 결과가 실제 결과에 근접하지만, 예측 결과가 실제 결과를 중심으로 넓게 분포 되어있음
- 왼쪽 하단 : 정확한 결과에서는 벗어나지만, 예측이 특정 부분에 집중 되어있음
- 오른쪽 하단 : 예측 결과가 실제 결과에 매우 상이하고, 결과를 중심으로 넓게 분포 되어있음
그렇다면, 편향 및 분산이 도대체 무엇일까요?
- 편향 (Bias) : 추정 값 (Algorithm Output)의 평균 값과 참 (True) 값들 간의 차이 → 참 값과의 거리
- 분산 (Variance) : 추정 값 (Algorithm Output)의 평균 값과 추정 값 (Algorithm Output)들 간의 차이 → 추정 값들의 흩어진 정도
종속변수와 독립변수의 관계로 세상의 모든 것을 선형적으로 표현이 불가능한 경우가 상당히 많습니다. 이에 피처의 직선적 관계가 아닌 복잡한 다항 관계 (곡선)를 모델링 할 수 있습니다. 하지만 다항 회귀의 차수가 높아지면 높아질수록, 학습데이터에만 학습이 되어 정확도/예측도가 떨어지는 경우가 상당합니다.
즉, 차수가 높아지면 과적합이 발생하는 문제가 커집니다.
아래와 같은 예시를 통해 알아보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
%matplotlib inline
# 임의의 값으로 구성된 X값에 대해 코사인 변환 값을 반환.
def true_fun(X):
return np.cos(1.5 * np.pi * X)
# X는 0부터 1까지 30개의 임의의 값을 순서대로 샘플링한 데이터입니다.
np.random.seed(0)
n_samples = 30
X = np.sort(np.random.rand(n_samples))
# y 값은 코사인 기반의 true_fun()에서 약간의 노이즈 변동 값을 더한 값입니다.
y = true_fun(X) + np.random.randn(n_samples) * 0.1
plt.figure(figsize=(14, 5))
degrees = [1, 4, 15]
# 다항 회귀의 차수(degree)를 1, 4, 15로 각각 변화시키면서 비교합니다.
for i in range(len(degrees)):
ax = plt.subplot(1, len(degrees), i + 1)
plt.setp(ax, xticks=(), yticks=())
# 개별 degree별로 Polynomial 변환합니다.
polynomial_features = PolynomialFeatures(degree=degrees[i], include_bias=False)
linear_regression = LinearRegression()
pipeline = Pipeline([("polynomial_features", polynomial_features),
("linear_regression", linear_regression)])
pipeline.fit(X.reshape(-1, 1), y)
# 교차 검증으로 다항 회귀를 평가합니다.
scores = cross_val_score(pipeline, X.reshape(-1, 1), y, scoring="neg_mean_squared_error", cv=10)
# Pipeline을 구성하는 세부 객체를 접근하는 named_steps['객체명']을 이용해 회귀계수 추출
coefficients = pipeline.named_steps['linear_regression'].coef_
print('\nDegree {0} 회귀 계수는 {1} 입니다.'.format(degrees[i], np.round(coefficients, 2)))
print('Degree {0} MSE 는 {1} 입니다.'.format(degrees[i], -1*np.mean(scores)))
# 0 부터 1까지 테스트 데이터 세트를 100개로 나눠 예측을 수행합니다.
# 테스트 데이터 세트에 회귀 예측을 수행하고 예측 곡선과 실제 곡선을 그려서 비교합니다.
X_test = np.linspace(0, 1, 100)
# 예측값 곡선
plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model")
# 실제 값 곡선
plt.plot(X_test, true_fun(X_test), '--', label="True function")
plt.scatter(X, y, edgecolor='b', s=20, label="Samples")
plt.xlabel("x"); plt.ylabel("y"); plt.xlim((0, 1)); plt.ylim((-2, 2)); plt.legend(loc="best")
plt.title("Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(degrees[i], -scores.mean(), scores.std()))
plt.show()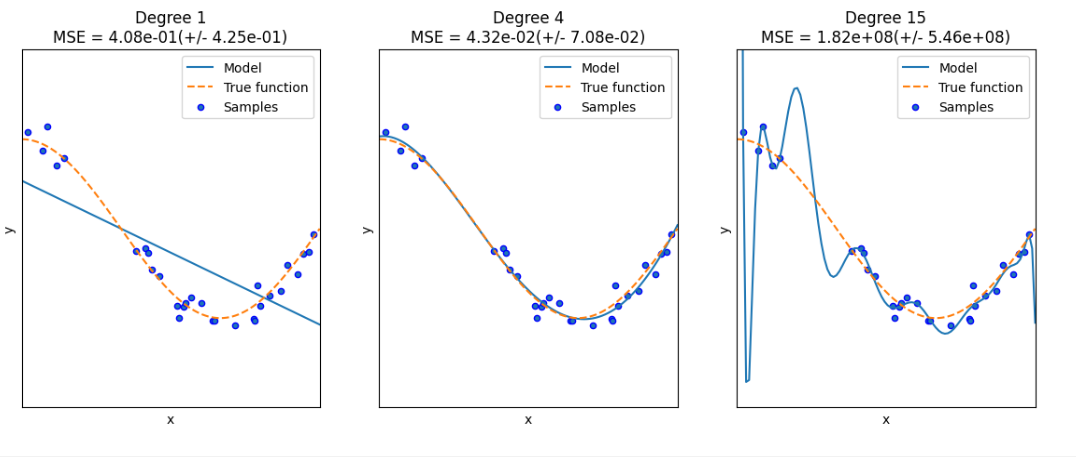
선형 회귀모델 (Degree = 1) Underfit
-. 실제 데이터 셋인 코사인에 대한 패턴을 제대로 예측하지 못함 (High Bias)
-. 지속적으로 데이터가 유입되어도, 형태는 크게 바뀌지 않음 (Low Variance)
다항 회귀모델 (Degree = 4) Trade-off Fit
-. 예측 곡선을 완벽하게 예측함
고차 다항함수 회귀모델 (Degree = 15) Overfit
-. 주어진 데이터의 Trend에 대해 잘 설명하고 있음 (Low Bias)
-. 데이터의 모든 특성 (에러/노이즈 등) 반영하게 되면서 복잡한 모델; 데이터가 유입된다면 형태가 바뀔 가능성 높음
※ 다시 한번 Bias 및 Variance에 대한 정의를 살펴보겠습니다.
- Bias : 실제 데이터 셋의 모든 정보를 고려하지 않아, 잘못된 것에 대한 학습을 하는 경향 → Underfitting (과소적합)
- Variance : Error 및 Noise 까지 포함하는 Flexible Model으로 인하여, 실제 데이터 셋의 패턴과 관계 없는 것까지 학습 → Overfitting (과대적합)
서론이 너무나도 길었네요...
앞서, Bias 및 Variance에 대해 알아보았으니, Bias Variance Trade Off 관계에 대해서 알아보겠습니다.
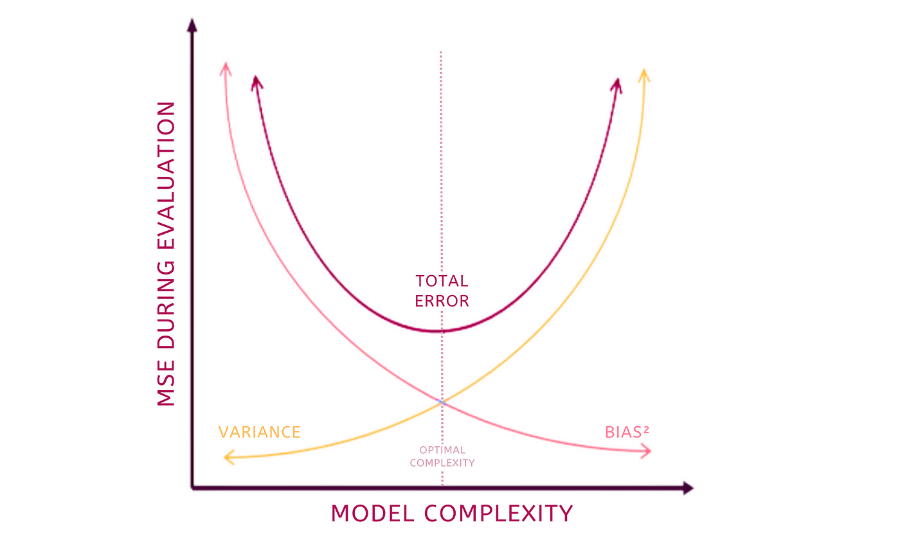
편향과 분산은 하나가 높아지면 하나는 작아지므로 반비례합니다. 즉, 편항이 높으면 분산이 낮아지고 (과소적합) 반대로 분산이 높으면 편항이 낮이지는 (과대적합) 현상을 Bias-Variance Trade Off 라고 부릅니다. 이에 편향과 분산이 적절하게 만족하는 구간을 찾아, 오류 Cost 값이 최대로 낮아지는 모델을 구축하는 것이 가장 중요하다고 볼수 있습니다.
'Data Science > ML' 카테고리의 다른 글
| 회귀분석이란? (0) | 2023.11.07 |
|---|

